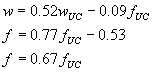Volume 4, Number 1, Fall 2003

Correlation Between Uniaxial and Biaxial Compensation Data for Architectural Fabrics

Slade Gellin
Department of Technology

Buffalo State College

Buffalo, NY 14222

Email: gellins@buffalostate.edu

ABSTRACT

A linear regression model was formulated to relate biaxial compensation data for four architectural fabrics with uniaxial data from both the manufacturer and the construction company employing the fabric in its tensioned structures. Good correlation was generally found with the construction company data. The results of the study can be used as justification for reducing the amount of testing necessary to determine biaxial compensations for these materials.

INTRODUCTION

The design and manufacture of tensioned fabric structures have a well-documented history¹. Central to the design of these structures are the material properties of the fabric used. The fabric portion of the structure is generally pre-loaded biaxially in tension in order to give it stability of shape and resistance to live loads². The process of taking flat panels of fabric that will later assume the three-dimensional shape of the structure (, known as patterning³,) must take include stretching the fabric during installation and final assembly of the structure. This induced strain in the fabric is usually referred to as compensation. In order to ensure that the fabric will be properly pre-stressed when installed, the compensations for the desired pre-stress must be determined reasonably accurately.

The most prevalent fabric in use today for non-pressurized tension fabric structures is PTFE coated glass fibers. These materials usually are sold in rolls of 12 feet in width and in lengths up to several hundred yards. The glass fibers in the warp or length direction are generally “straight,” while those in the fill or width direction are woven in between the warp fibers. This causes the fabric to be considerably stiffer in warp than in fill.

The manufacturer of the fabric generally supplies uniaxial compensation data for both warp and fill at a stress (actually, a stress resultant) of S_U for each roll of fabric it delivers to a major construction company that designs and builds tensioned fabric structures. The sample of fabric used for the test comes from one end of the roll. The construction company assumes that the loading conditions on the fabric are different at the end of the roll than in the middle of the roll. The construction company generally repeats the uniaxial test in the middle of the roll and then does a biaxial test with a specimen adjoining those used for its uniaxial tests. The biaxial test is designed to approximate the conditions of initial installation, settling under moderate live loads and future extreme live loading⁴, though it is not done under the auspices of any standard test method⁵. Typical results of the biaxial test are shown in Figure 1. From these results, an engineer can choose a value for warp and fill compensations for the design pre-stress S_P.

Figure 1: Typical Biaxial Test Results

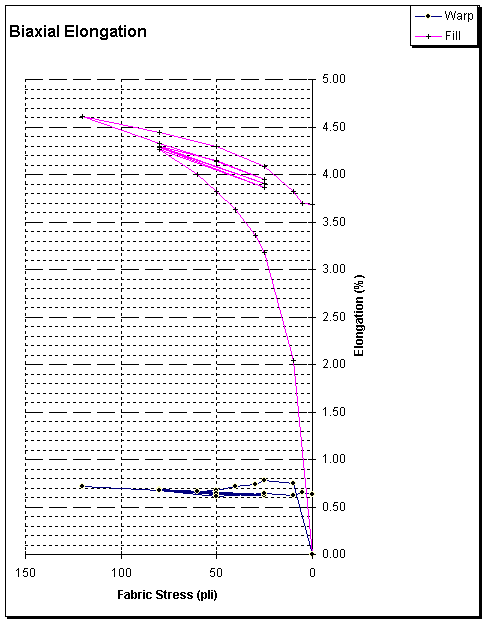
The uniaxial tests generally require an hour to perform, while the biaxial tests require about six hours to perform. For a large project that may use dozens of rolls of fabric, the cost in time and money can be prohibitive if each and every roll is tested this way. Furthermore, the internal location of the specimens used in testing may result in significant waste of fabric if the designed flat panels cannot be efficiently nested in the length between the end of the roll and the specimen location.

Over time, the construction company developed several informal rules to limit its need for testing on large jobs. Generally, it took the set of rolls assigned to a project and calculated the sum of the warp and fill uniaxial compensations as supplied by the manufacturer. It then grouped the rolls in informal sub-groups, usually three, based on these values. It then took one “typical” roll from each sub-group and performed the full biaxial testing on that roll, and used the values of the biaxial warp and fill compensations obtained from the test and applied them to all rolls in the sub-group. No studies were performed to verify if this was a feasible strategy to employ.

A study was undertaken to determine empirical formulas for warp and fill biaxial compensations in terms of uniaxial compensations determined by the manufacturer and the construction company for four different PTFE coated glass fabrics sold by the manufacturer. These formulas were examined using methods of statistical inference in order to determine their validity and their implications for possible substitution for costly testing. This paper reports on the results of that study.

METHODOLOGY

Formulas in the form

are derived for biaxial compensations, where y represents either a warp (w) or fill (f) biaxial compensation; w_U and f_U represent the uniaxial warp and fill compensations, respectively, with the x subscript being either M for the manufacturer data or C for the construction company data; and W_y, F_y and C_y represent the coefficients of the linear (least squares error) fit for the quantity y.

Each formula will be evaluated for its feasibility in approximating the given quantity y. The following statistical measures will be calculated and evaluated for each of the formulas:

The coefficient of determination: Labeled R², the coefficient of determination measures the fraction of the variance of the data that can be explained with the derived formula (as opposed to other factors). Values above 0.9 will be deemed excellent; between 0.8 and 0.9 as good; between 0.7 and 0.8 as fair; and less than 0.7 will be deemed poor.
The F-statistic and its associated level of significance: The F-statistic and its associated level of significance measure the probability that the derived formula is useful, rather than due to sheer chance. A 5% level of significance will be chosen as a benchmark. This means that the probability that the formula works as well as it does due to chance is less than 5%. There is a critical value that the F-statistic must exceed associated with this level of significance. This value varies as the number of variables and number of data points vary.
The t-statistic and its associated level of significance for each of the W, F and C coefficients: The t-statistic for a coefficient measures the probability that its associated variable is actually important in the formula. A 5% level of significance will be chosen as a benchmark; that is, the risk in ignoring that particular variable in the formula will be less than 5%. For those formulas that have a qualifying F-statistic, alternate, simpler formulas will be investigated when the t-statistic is not met for a particular variable.

This process will be repeated for the four materials, labeled Material 1, 2, 3 and 4. The number of the material determines its rank in importance (as far as usage is concerned) to the construction company with Material 1 being the most used. Data used in the study was limited to those rolls that have undergone the standard biaxial test at the construction company test facility. The choice of biaxial compensations assigned based on the tests was determined on a consistent basis by the vice president of engineering for the construction company, who has over 20 years experience in the tensioned fabric structures business.

RESULTS

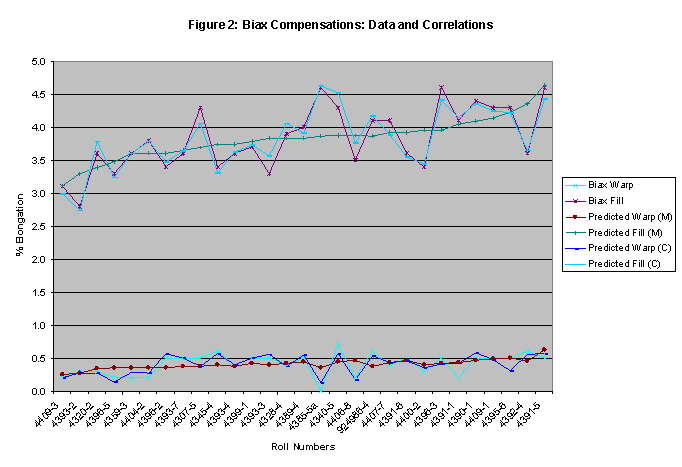
The results of the study are presented in Tables 1 – 4 for Materials 1 – 4, respectively. The tables list the derived coefficients, their respective t-statistics, as well as the other statistics associated with linear fit. For example, in Table 1, the upper left section refers to the relationship between the biaxial warp compensation vs. the uniaxial data provided by the manufacturer. The formula derived is:

All the t-statistics for the coefficients (0.23, 0.06, -0.37) are below the threshold of 1.71, indicating that the biaxial warp is not strongly dependent on either of the variables w_UM or f_UM, nor is it strongly dependent on the additive constant term. The R² value of 0.19 indicates that the entire formula is a relatively poor fit. The F-statistic provides additional confirmation of the poor fit. The upper right section refers to the relationship between the biaxial warp compensation vs. the uniaxial data based on construction company tests. Here, the formula derived is:

The t-statistic on the first coefficient (0.54) is quite high, indicating that w is strongly dependent on w_UC, while the other t-statistics are below the threshold of 1.71, indicating that their contribution to the above formula is not as critical. This indicates that a simpler formula for w, perhaps only dependent on w_UC, may give comparable R² and F-statistic values. The lower portion of the table summarizes comparable results for the biaxial fill compensation.

With one exception, the results imply that the correlation of biaxial compensations with construction company uniaxial data is clearly superior to the correlation with manufacturer uniaxial data. While it was expected that the construction company data would correlate better than the manufacturer data, due to the fact that the samples for the tests were cut from the same location on the roll, the difference in the statistical measurements between the correlations was surprisingly large.

Table 1 is typical of the results obtained. First, it is noted that for both sets of uniaxial data that the fill correlation is better than the warp correlation. This could be a direct result of a narrower

Table 1: Results for Material 1
	vs. Manufacturer	vs. Company
	Data	Data
Warp Compensation:
W:	0.23	0.54
(t-Statistic)	1.67	8.43

F:	0.06	-0.04
(t-Statistic)	1.12	1.21

C:	-0.37	-0.30
(t-Statistic)	1.13	1.63

t-Statistic Threshold for 5%	1.71	1.71

R²	0.19	0.74

F-statistic	3.08	36.80

F-statistic threshold for 5%	3.37	3.37


Fill Compensation:
W:	0.46	0.08
(t-Statistic)	1.37	0.85

F:	0.44	0.87
(t-Statistic)	3.38	16.54

C:	0.35	-1.19
(t-Statistic)	0.43	4.10

t-Statistic Threshold for 5%	1.71	1.71

R²	0.42	0.92

F-statistic	9.51	158.11

F-statistic threshold for 5%	3.37	3.37

Table 2: Results for Material 2
	vs. Manufacturer	vs. Company
	Data	Data
Warp Compensation:
W:	0.74	0.63
(t-Statistic)	5.84	17.25

F:	0.16	-0.05
(t-Statistic)	2.70	1.65

C:	-1.97	-0.48
(t-Statistic)	3.95	2.54

t-Statistic Threshold for 5%	1.76	1.76

R²	0.71	0.96

F-statistic	17.14	188.35

F-statistic threshold for 5%	3.74	3.74


Fill Compensation:
W:	-0.31	0.23
(t-Statistic)	1.10	3.10

F:	0.17	0.79
(t-Statistic)	1.34	12.82

C:	2.83	-1.26
(t-Statistic)	2.54	3.20

t-Statistic Threshold for 5%	1.76	1.76

R²	0.27	0.92

F-statistic	2.53	84.10

F-statistic threshold for 5%	3.74	3.74

Table 3: Results for Material 3
	vs. Manufacturer	vs. Company
	Data	Data
Warp Compensation:
W:	0.09	0.58
(t-Statistic)	0.77	7.47

F:	-0.03	-0.07
(t-Statistic)	0.47	3.69

C:	0.28	-0.17
(t-Statistic)	0.84	1.04

t-Statistic Threshold for 5%	1.73	1.73

R²	0.04	0.81

F-statistic	0.38	38.09

F-statistic threshold for 5%	3.55	3.55


Fill Compensation:
W:	0.60	0.07
(t-Statistic)	1.60	0.20

F:	0.61	0.77
(t-Statistic)	3.60	15.24

C:	-0.64	-0.65
(t-Statistic)	0.62	1.57

t-Statistic Threshold for 5%	1.73	1.73

R²	0.48	0.93

F-statistic	8.30	116.97

F-statistic threshold for 5%	3.55	3.55

Table 4: Results for Material 4
	vs. Manufacturer	vs. Company
	Data	Data
Warp Compensation:
W:	-0.02	0.04
(t-Statistic)	0.63	0.28

F:	-0.09	-0.06
(t-Statistic)	3.78	1.78

C:	0.13	-0.02
(t-Statistic)	0.08	0.12

t-Statistic Threshold for 5%	1.80	1.80

R²	0.60	0.24

F-statistic	8.08	1.72

F-statistic threshold for 5%	3.98	3.98


Fill Compensation:
W:	-0.59	-0.37
(t-Statistic)	2.24	0.68

F:	0.44	0.68
(t-Statistic)	0.18	6.16

C:	0.67	-0.18
(t-Statistic)	1.14	0.42

t-Statistic Threshold for 5%	1.80	1.80

R²	0.46	0.79

F-statistic	4.66	20.12

F-statistic threshold for 5%	3.98	3.98

range of warp compensations for the roll data, yet larger relative variance due to rounding off to the nearest tenth of a percent. For installation purposes, it is probably more important to have a good handle on the fill compensation, as it is easier to pull the fabric in that direction. The values of R² indicate a poor correlation with manufacturer uniaxial data for both warp and fill biaxial compensations, though it is interesting to note that the coefficients for fill are nearly equal, lending some credence to the method of grouping the rolls based on the sum of the uniaxial warp and fill values. The values of R² for the construction company data indicate fair correlation in warp and excellent in fill, with correspondingly large values of the F-statistic.

Figure 2 is a plot of the biaxial compensations for the rolls of Material 1 used in the data as well as the predicted values using the formulas of Table 1. The plot graphically demonstrates the superiority of correlation with construction company data. It should be noted that the rolls are listed from left to right with increasing sum of reported manufacturer uniaxial compensations.

The t-statistics on the coefficients for the correlations with construction company data indicate that perhaps the uniaxial fill value is not important in determining the biaxial warp value, as well as the uniaxial warp value is not important in determining the biaxial fill value. Without too much penalty, the following simplified formulas may be used:

Table 2 is similar to Table 1 in fill, but surprisingly good correlation is obtained in warp for both sets of uniaxial data, including an incredible R² value of 0.96 for the correlation with the construction company data. Based on the t-statistics, this formula can be simplified as:

Table 3 yields similar results to Table 1, though the warp correlation with manufacturer data is virtually non-existent. Possible simplified formulas are:

Material 4 is unusual in that its biaxial warp compensation is usually negative. As indicated in Table 4, this is the one instance in this study where correlation with manufacturer data, though not great, is superior to that with construction company data. The biaxial fill compensations follow qualitatively the pattern of the other materials, though the correlation with construction company data is not as strong as with the other materials. This formula could be simplified as:

Though not reported in detail herein, it should be noted that correlations of the two sets of uniaxial data with each other were generally poor for all materials.

The uniaxial compensation data as provided by the manufacturer is of little value in predicting biaxial behavior of PTFE coated glass fiber materials. A decision to completely discard biaxial testing based on estimates derived herein would be highly risky at best.

On the other hand, the uniaxial compensation data as determined by construction company testing generally correlates well in predicting biaxial behavior, with the exception of the warp compensation for Material 4. Performance of the less expensive uniaxial tests on each roll may be adequate in lieu of both uniaxial and biaxial testing.

1. R.E. Shaeffer, ed. (1995) Tensioned Fabric Structures: A Practical Introduction. Prepared by the Task Committee on Tensioned Fabric Structures, Technical Committee on Special Structures, and Technical Committee on Metals of the Structural Division of ASCE.

2. M.R. Barnes, “Form Finding of Minimum Surface Membranes,” IASS Conference, July 1976.

3. S. Gellin, “Patterning of Tensioned Fabric Structures,” Proc. 5^th International Conference of Engineering Design and Automation, Las Vegas, NV, August 2001, pp. 482-487.

4. H. Minami and S. Motobayashi, “Biaxial Deformation Property of Coated Plain-Weave Fabrics,” Proc. Vol. 1, International Symposium on Architectural Fabric Structures, Orlando, Nov. 1984.

5. C.G. Huntington, “The Tensioned Fabric Roof,” ASCE Press (to be published January, 2004).