

Learning Problem Solving for Effective Professional
Development
of Engineering, Management and Technical Personnel
Hamid Khan
Master of Technology
Program
Northern Kentucky
University
Highland Heights, KY
41099
Email: ahkhan@tech.purdue.edu
Abstract
Theory and practice are not dichotomous entities. Students in engineering problem problem-solving class find it difficult when they do not possess practical engineering experience in a job, but are asked to apply theory to practice. Such dilemmas occur in a senior level Operations Management course, which discusses complex problems of Linear Programming. The difficulty involved in such kind of problem solving is compounded by lack of experience of the student and lack of initiative to connect the problem to self-experience. This connection to the real world is possible in three ways: Theory for the sake of theory, Theory in Practice (theory is embedded in practice), Theory and Practice for emancipation (Theory and Practice are a two-way street managing and controlling each other).
One student’s interest in exploring theory and linking it to practice has been explored in this paper by development of a concept of elegant problem solving in Industrial Technology majors from theory to practice. In studying Industrial Technology subjects, where the rigor is not on mathematics or deep concepts, but rather on problem solution and applications for being “practical”, technology students are exposed to some classical techniques of Industrial Engineering, Production and Operations Research, and Engineering Economics problems and were then tested for practical applications. This “praxis” called, “elegant solutions”. Although some good students “all too often “pick up” problem solving skills through experience or as a bye product of doing exercises,” they do not learn the problem solving strategies for “practical and elegant solutions.” Thus a “practical and elegant” solution has been tested in class.
Introduction
This statement may seem to imply that effective teaching and learning will lead to effective problem solving abilities of the students. In fact, it does. There is no confusion in this statement that “Problem solving effectiveness is the direct result of Teaching and Learning Effectiveness.” Effective teaching and learning could start from grasping the simplest problem for the child or may be even intended to train the “mentally retarded person” to sort colored blocks into bins. In fact, colored blocks have been used in ergonomic studies to study the effectiveness of assembly line workers. Colored coded transistors with various combinations of color-coded stripes indicating good and bad transistors have been used in ergonomic research studies. In assembly set ups the color-coded transistors have been used for the study of muscle and eye coordination and productivity studies, where the assembly line worker will be able to discriminate between the good and bad transistors by color code attributes under the various conditions of belt speed. The successful formulation of simplest problems is the hallmark of solving more complex problems for the child, adolescent and grown up students. Simplest problems are elaborated for effective teaching of complex problem solving. It also has something to do with appropriate methodology used for the individualized instruction developed for specific problem solving algorithms. Effective teaching and learning styles will provide an algorithm to grasp the bird’s eye-view of a complex problem and apply it in the real world. This paper focuses on problem solving directly as an offshoot or “byproduct” of effective teaching and learning in general.
Although the title implies the development of an "elegant" problem-solving model the paper will discuss and explore the role of effective teaching and learning in general and in particular its effect on learning the art and science of problem-solving. Students’ learning of the art of problem solving, and the application of this approach to the development and solution of a student-conceived project, contribute to the concrete and “elegant problem solving". The higher-level learning concepts will be translated to efficient and elegant solutions for applications. The student learning effectiveness will be analyzed from the firm evidence, that they learned the theory and they can apply it to practice.
Use of “Elegant” and Applied Problem Solving Model in Classroom
McDanield’s1 model has helped us understand the curricular requirement and the urgency of the student learning to be applied to an industrial setting. A course entitled Production Management was selected for this purpose of analysis and the course was modeled such that at least, three of the main criteria will be addressed for input and tested for outcome of the course. The course was made more outcomes driven that input driven. The student application was stressed to solve an “elegant real life problem” pressing in a student’s real life situation. The topic that was selected for experimentation was the use of Linear Programming and its application to student life. Very naïve as well as very sophisticated models were used for student learning outcomes. The students worked for four weeks on developing a model for their use and application using such naïve to the more advanced and scientific solutions. These problems were solved long hand first by the students to appreciate and apply the science behind the topics and then finally they ran a computer simulation and solution using POM-software, to verify results to present to the class. The level of interest demonstrated by the students was conducive to this research. And the project of collecting, formulating and solving an industrial/ individual problem was greatly facilitated by the application of the following course objectives of learning. Taken from McDanield’s research, participation and application level was very high because all the students felt, at the end of their involvement that:
Course Materials did help them to
· See the means of affecting the direction of change
· Incorporate classroom learning into their immediate environment.
The gradual development of the model is presented below, as applied by students to their own particular problem setting.
A student in IT442: Production and Operations Management class was having difficulty in attending classes regularly due to various reasons: disinterested in pure theory, non-challenging classes causing boredom, chronic depression and anxiety in life, wearing different hats in three different jobs, frequent interviews as a graduating senior, and many hours of course load on top of those. Can the student learn to solve individual real life problem using the theory learned in this class? Can the student learn the concept and application of linear programming to see what is the optimal level of performance in life could be? Can the student apply theory prudently?
The student’s solved problem is appended at the end of the paper. Practical deliberation found its roots in the disposition of the student to act truly, rightly, wisely to enliven commitment. This proves the following important parameters of learning have been influenced.
· Course Materials did help her not to feel powerless.
· Course Materials did help her incorporate classroom learning into her immediate environment.
The class did three Maximization Problems and Three Minimization problems. Many students had difficulty in formulating the problems with respect to resources and constraints in a verbally worded problem. When these problems were converted to their own problems at jobs they could easily visualize the problems and solve them. They had real interest in promoting themselves in their jobs. This course Materials did help them transfer classroom learning to their responsibilities.
Model’s Usefulness and Effectiveness
With respect to these above important contributions to the paradigms of inquiry, the “Elegant” Problem Solving Model is readily applicable to the usefulness and effectiveness of teaching. Rubinstein2 suggests that, “Although the vehicles used to teach problem solving may vary slightly from instructor to instructor, all instructors include the following aspects in problem solving in general:
· Tools for problem representation
· Models as aids to thinking
· Identifying personal problem solving styles
· Learning to overcome conceptual blocks
· Dealing with uncertainty
· Focusing on the process of problem solving
· Decision making, individual and group
· The role of values in problem solving
· The holistic and interdisciplinary nature of human problem solving
In the line of “Patterns of Problem Solving” as enunciated by Rubinstein2 we made the following efforts to imitate the setup of a problem-solving classroom. This tries to offer an environment for the following human values:
· To develop a general foundation of problem solving approaches and master some specific techniques.
· To provide a foundation for attitudes and skills productive in dealing with problems in the context of human values.
· To emphasize the thinking process at all stages of the problem solving activity.
· To identify individual problem solving styles and learn to overcome conceptual blocks and self imposed constraints.
· To expose students to both objective and subjective aspects of problem solving.
· To provide a framework for a better appreciation of the role of tools and concepts that the students may have acquired or will acquire.
· To bring together students from diverse backgrounds so that they can observe different attitudes and problem solving styles and learn from each other.
Hence, teaching effectiveness in the classroom is essentially effective problem solving and decision making in the classroom. According to Barnard3, the philosophy of effective teaching applied to classroom effectiveness for a timely problem-solving course is:
“The fine art of effective decision making (teaching) consists in not deciding (teaching) those things that are not now pertinent, not deciding (teaching a subject matter) prematurely, not deciding (teaching) those things that cannot be made effective, and not deciding (teaching) those things that others should make (teach).”
Suggesting some guiding principles for the fine art of effective problem solving in the classroom, Rubinstein2 expresses the following sentiment of an effective mentor.
· If you really want your students to learn a concept, give them an opportunity to teach you, the teacher.
· If a group of students is highly motivated and learns well, stay out of their way. Do not teach them; let them teach you.
· Concentrate on a small number of concepts, and dig deeply into their implications in as wide a field as possible.
· Make explicit the connection between knowledge and its application whenever possible.
· Show respect for the learners by preparing for each session.
· Encourage questions. Some questions are so outstanding that they should not be spoiled by an immediate answer; we should take time to ponder them. If this is the case, tell the students.
· Learn the names of your students. This is one of the best ways to motivate them and gain their respect.
· Do not tell a class: “We are behind.” Your plan might have been unrealistic. Each class is unique; adapt your plans to the class and you will always be “on schedule,” whatever it may be.
· When you explain something, seek feedback by asking: “Did I make myself clear?” This is better than: “Did you understand?”
· Do not express doubt about the learner’s abilities to learn.
Barnard3 in discussing the teaching effectiveness as an art of managing (student) human affairs continuously in the classroom says that the governing precepts are:
· At the time of communication the recipient must be psychologically and intellectually capable of executing the task (of learning). A little impossibility here is a total possibility.
What we learn from “Praxis”
Authors like Argyris6 and Schon7 have extensively demonstrated the link of theory and practice for increasing professional effectiveness. Cervero8 has also written extensively on teaching effectiveness and continuing professional development of ET professionals engaged in teaching. And Carr and Kemmis4 have written a treatise on becoming critical thinkers for the classroom by examining applying ‘praxis’ or informed action.
This ‘praxis’ framework is the most promising one, according to Carter5. For functioning in professional practice, Carter says that the effective teacher/practitioner must be an astute student of his/her work environment, which testifies to the theory practice two-way street. He also contends that academic preparation of practitioners should help the students in professional practice, which is theory embedded in practice. He also promises that systematic inquiry is the hallmark of successful practice, which testifies that learning and practice are inseparable.
In conclusion, the theory-practice debate will continue to go on but the most applicable paradigm of problem solving will depend on ‘praxis’, which strikes a balance between the two ends – the theory is embedded in practice.
This paper has now examined, the constructs and philosophical approaches of the schools of thought in problem solving in engineering and technology (E-T). It also tried to look into the major frameworks of constantly changing relationships between theory and practice. Critically examining these frameworks, an effort was made to see if any one of the frameworks has contributed most to the body of knowledge in E-T education, and which one holds the most promise for the future. The theory embedded in practice called ‘praxis’ is the most promising of all, which was used in the classroom and which elicited most elegant solutions from its participants.
The author wants to thank his Operations Management students for working on elegant solutions for this paper. The author wishes to thank one of his students who contributed most to this study of project-based classroom “praxis”. The student’s name from the assignments has been kept anonymous but credit is hereby acknowledged.
Reference
[1] McDanield, M. A. (1974). Tomorrow’s curriculum today. In Alvin Toffler (Ed.) Learning for Tomorrow: the role of the future in education, Vintage Books.
[2] Rubistein, M. F. (1980). A decade of experience in teaching an interdisciplinary problem solving course. In Tuma and Reif (Eds.) Problem solving in education: Issues in teaching and research. Lawrence, Erlbaum Associates publishers
[3] Barnard, C. I. (1978). Functions of the executive. MIT press. Revised edition.
[4] Carr, W., and Kemmis, S. (1986). Becoming critical: Education, Knowledge and Action Research. London: Falmer. (chapters. 2,3,& 5)
[5] Carter, G. (1983). A perspective on preparing adult educators. In S.M. Grabowski (Ed.) Strengthening connection between education and performance, New directions for continuing education (pp.73-82), Jossey-Bass.
[6] Argyris, Chris. (1976). Increasing leadership effectiveness. New York: Wiley.
[7] Schön, Donald A. (1974). Theory in practice: increasing professional effectiveness. San Francisco : Jossey-Bass.
[8] Cervero, Ronald M. (1988). Effective continuing education for professionals. San Francisco : Jossey-Bass.
|
Hamid Khan is an Associate Professor of Technology Management with Northern Kentucky University. He teaches graduate courses in Technology and Management in their Master of Technology Program. He received his BS Degree in Mechanical Engineering from Utkal University, MS Degree in Industrial Engineering from the University of Nebraska-Lincoln, MBA Degree in Operations Management from University of Texas at San Antonio, and a Doctor of Education Degree from Ball State University. Hamid is a registered professional engineer and is active in TAC of ABET program evaluations thru the ASME. He has been active in ASEE and FIE since 1991. His research and teaching interests are in Teaching Effectiveness, and Professional Development of Engineering, Management and Technical personnel. Hamid has published about thirty-five peer reviewed technical proceeding papers in ASEE, FIE annual proceedings as well as peer reviewed articles in the Journal of Engineering Technology, and Computers in Education Journal. |
Appendix A (below): A student project as envisioned and solved by the student after learning optimization.
Maximization Problem defined: XYZ is graduate student and a consultant who repairs computers and also designs web pages to put herself through graduate school. She must utilize her weekly working hours efficiently to achieve optimal performance, and must complete all work by their firm deadlines. She cannot work more than 40 hours per week and can afford only 10 hours of daytime work a week due to school requirement. Please see table below for constraints.
Minimization Problem defined: XYZ is a full time graduate student and a teaching assistant. She must utilize her weekly working hours efficiently to achieve optimal performance, and must complete all work by their firm deadlines. She cannot work more than 40 hours per week and is enrolled in 12 hours of class, which should be further allotted two hours for every hour in class. The costs are $8/hr as the cost for her job and $53/hr for 36 hours of schoolwork (Tuition = $1936/36 hours). She must sleep at least 8 hours every night, all week to be at a healthy working condition (56 hours). She can only work execution hours M-F 7:30 am – 5:30 pm (10 hours a day). Please see table below for constraints.
Pictorial slides of the elegant problem solution steps follow.

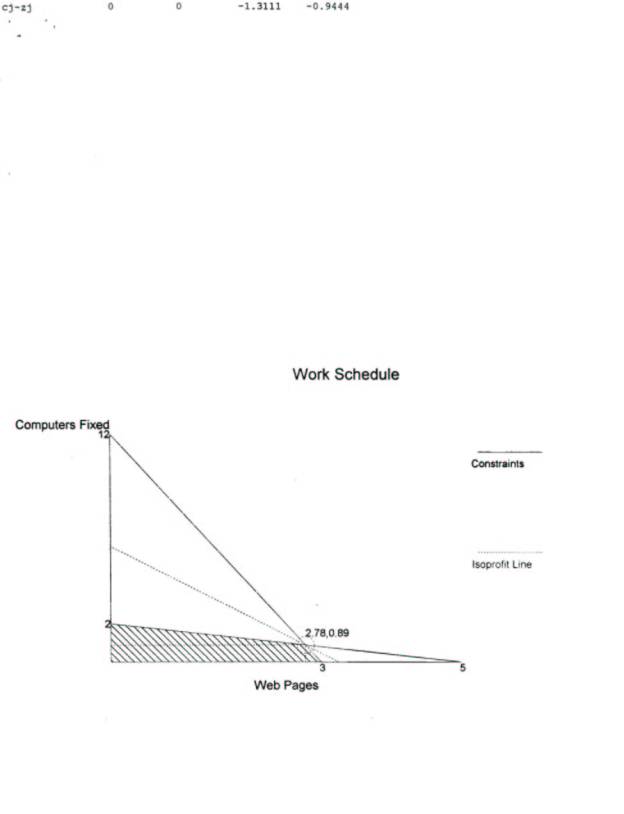
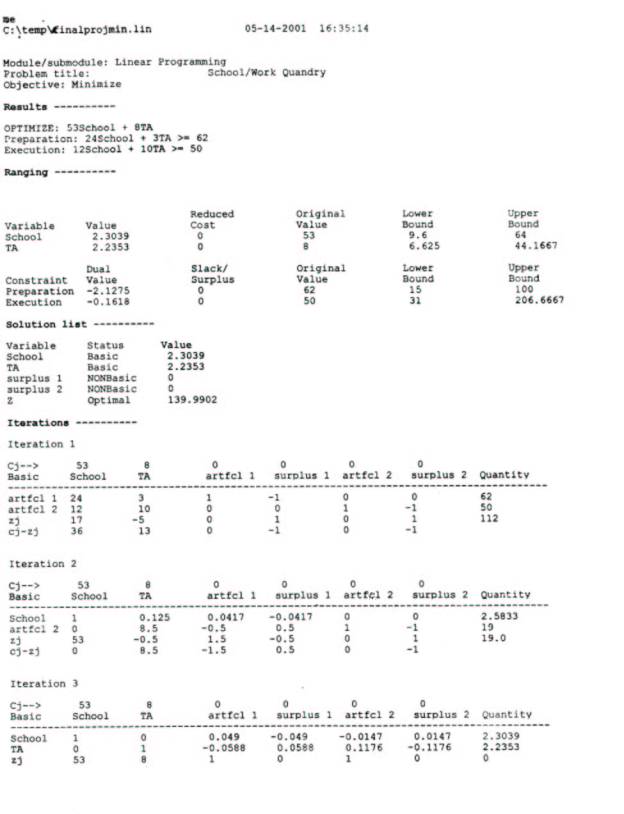


**********************************