Volume 4, Number 2, Spring 2004

FlexPDEÒ: A Useful Tool for the Numerical Solution of Partial Differential Equations

Wael M. G. Ibrahim

ECPI College of Technology,

Computer Electronics Department,

5555 Greenwich Road,

Virginia Beach, VA 23462

Email: wibrahim@ecpi.edu

 
ABSTRACT

In this paper, the author reports on the use of commercially available software, FlexPDEÒ from PDE Solutions, to numerically solve the parabolic two-temperature model (TTM). Ultrafast time-resolved pump-probe studies of energy relaxation and transport in polycrystalline gold films are conducted. The experimental results are analyzed within the framework of the two-temperature model (TTM). A description of the problem descriptor file and a comparison of the model results to the experimental ones are presented. Model predictions show good agreement with the transient thermoreflectivity experiments on thin gold films.

 

INTRODUCTION

The study of laser-material interaction is of utmost importance for many industrial processes such as laser annealing, thin film deposition, and micro-machining. Over the past decade, many reports are available in the literature on experimental investigations of non-equilibrium electron dynamics in metals carried out using several techniques. Picosecond and femtosecond time-resolved thermomodulation reflectivity and transmissivity (TTR)1-4, surface-Plasmon resonance (SPP)5,6, time-resolved two-photon photo-emission(TPPE)7,8,9 and recently single-photon photo-emission10,11 are some of these techniques.

 

When a laser pulse, of a duration less than or comparable to the electron-phonon energy-loss time, is used to excite a metal surface, a transient non-equilibrium occurs between the effective electron temperature, Te, and the lattice temperature, Tl. Electron-electron scattering, electron-phonon scattering, and heat transport determine the subsequent equilibration of the electron gas and the lattice. Due to the large electron population, electron-electron interactions were assumed to be fast enough to thermalize the electron gas on a time scale shorter than the laser pulse duration, permitting a simple modeling of the electron thermalization dynamics using the classical Two-Temperature Model (TTM) which was initially proposed by Anisimov 12 as

 

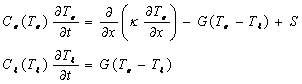                                             (1)

Where, k is the thermal conductivity (W/mK), Ce is the electron heat capacity (J/m3K), Cl is the lattice heat capacity (J/m3K), Te is the electron effective temperature (K), Tl is the lattice effective temperature (K), and G is the electron-phonon coupling coefficient (W/m3K).

Due to the nonlinear nature of the TTM, an analytical solution is not possible, and hence it has to be solved numerically. Several groups13-18 reporting on their studies of the electron dynamics in metals had to develop their own numerical procedure for the solution of the TTM or use existing subroutines in the IMSL libraries. In both cases, this requires familiarity with the mathematical algorithms and programming languages involved in the modeling. Not only that, but the code produced has to be unambiguous and structured in a clear manner as to allow any future users not involved in the original development to be able to modify or at least use the code. The programmer should also provide means for data obtained through the simulation to be properly displayed. Thus, the development time for the software is rather long.

 

FlexPDEÒ, on the other hand, offers a common platform that is not only capable of numerically solving the coupled nonlinear equations but requires little knowledge from the user about programming other than properly defining the physical problem. In this paper, we present a description of the problem descriptor file used to define the physical problem and compare the results of the numerical solution to our experimental results.

 

MODELING

Conventional programming languages utilize procedural problem descriptors? in which the user defines a sequence of steps to be executed in order to get to the solution. FlexPDEÒ, however, only requires the user to relate the various components of the system to one another to form what is known as a relational problem descriptor. Thus, a partial differential equations system, following the user’s description, is turned into a finite element model. FlexPDEÒsolves the system, and the results are presented graphically according to the specifications of the user.

 

In preparing the problem descriptor file, the user needs only to worry about the physical problem description,such as the set of partial differential equations, the variables, the system coordinates, initial values, boundary conditions, and finally the time domain over which the solution is sought. Several sections, each identified by a header, constitute the problem descriptor file. Some of the most frequently used sections are illustrated in Figure 1 below.

 

                                         TITLE ' '

SELECT

COORDINATES

VARIABLES

DEFINITIONS

INITIAL VALUES

EQUATIONS

CONSTRAINTS

BOUNDARIES

TIME

MONITORS

PLOTS

HISTORIES

END

 

 

Figure. 1. Main section headings of the problem descriptor file.

                              

Even though interlaced, these sections can be considered as divided into two main categories. The first one controls the program functionality as to the solution method, the coordinate system to be used, the grid size, etc.

 

This first category includes:

  • TITLE in which a descriptive label for the problem is given.
  • SELECT provides the user with an override to some of the default behavior of FlexPDE such as the relative PDE error, grid size, choice of Cranck-Nicholson, Galerkin or backward implicit schemes.
  • COORDINATES is where the user defines the coordinate system to be used.
  • PLOTS give the user a choice of the desired graphical output.These may be any combination of CONTOUR, SURFACE, ELEVATION or VECTOR plots19.

 

The second category involves the definition of the physical problem itself. In these sections, the user states the partial differential equation system, the variables associated with it, and finally the initial and boundary conditions.

 

The section headings are as follows:

  • VARIABLES is the section where the dependent variables are named.
  • DEFINITIONS is used to declare the numerical constants.
  • EQUATIONS is where each variable is associated with a partial differential equation.
  •  INITIALVALUES provide the starting values for nonlinear or time-dependent problems.
  •  BOUNDARIES describe the geometry by walking the perimeter of the domain, stringing together line or arc segments to bound the figure.
  • TIME section is used in time-dependent problems to specify a time range over which the problem is to be solved19.

 

FlexPDE® constitutes a complete problem -solving environment as it performs the entire range of functions necessary to solve partial differential equation systems19. The versatility of FlexPDE® relies on the ability to define the geometrical domain of the problem by a set of line and arc segments. In our model, thermal insulation boundary conditions were used so as to constrain the sides of the sample to the ambient temperature and neglect any heat losses from the back surface. The electron and lattice temperature were used as the two variables for which the equations are to be solved. The initial conditions for the electron and the lattice systems were chosen as Te = Tl = Ta =300 K. The physical properties of gold, Table 1, and the source term were specified in the Definitions section.

 

The results of the model are then exported to a text file that can be read by our data presentation software for comparison with the experimental results. However, the user has the ability, within FlexPDE®, to generate a number of graphical displays of the results through plots, surface, or contour graphs. Surface graphs can be rotated in 3-D which provides the user with a flexible way to view the progress of the solution on a more complex structure. FlexPDE® also supports the possibility of exporting the results to different visualization software such as Tecplot®. Figure 2 shows a screenshot of the FlexPDE window which is subdivided into several windows displaying the different variables specified by the user, e.g., lattice temperature and electron temperature.

 

Figure 2. A screenshot of FlexPDE

 

Table 1. Room temperature properties of gold

 

Au

 

Measured ‘G’ a

2.8 ± 0.5

x 1016 W m-3 K

Melting point b

1063

°C

 

Thermal conductivity ko b

 

315

W m-1 K

Electron heat capacity Ce b

2.1

x 104 J m-3  K-1

Lattice heat capacity Cl b

2.5

 x 106 J m-3 K-1

 

 

 

 

 

 

 

 

 

a From data in Ref. [13].

b Ref. [20].

EXPERIMENTAL RESULTS

Experimental investigations of ultrafast laser heating of thin gold films were performed using an ultrashort pulse laser system at the Center for Materials Research (CMR) at Norfolk State University (NSU). The laser system consisted of a commercial Ti:Sapphire (Mira 900) laser and a regenerative amplifier (RegA 9000) from Coherent.  The input to the experimental setup21 consisted of ~500mW pulses at 250 KHz repetition rate with a FWHM <200fs.The basic arrangement, Figure 3, is that of a collinear pump-probe setup.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Figure 3. Collinear pump-probe experiment.

 

The detection of the thermoreflectivity signal was achieved by modulating the pump beam intensity at a fixed frequency, W, and using a phase-sensitive detection scheme (lock-in). Differential detection was used so as to cancel out the fluctuations of the RegA output, leaving only the signal caused by the chopped pump beam. Thus, the lock-in detects modulations in the received probe intensity that is caused only by the effect of the pump on the sample. LabviewÒ from National Instruments was used as the control platform for the stage and the data acquisition.

 

Figure 4 shows a comparison between the time–resolved ΔR/R, where R is the reflectivity, of an 400 A° Au film and the predictions of the TTM during 120 fs laser pulse heating. Predictions from the TTM model show good agreement with the experimental results. The discrepancy in the initial rise is attributed to the assumption of an instantaneous thermalization of the electron gas on a time scale shorter than the laser pulse duration. Convolution effects have also been known to affect the rise time of the thermomodulation signals. These effects have been corrected22, and the results are also shown in Figure 4.

 

Figure 4. Comparison between the experimental results, the TTM, and the model taking into effect convolution and thermalization effects for Au 40-nm, laser incident fluence was

2.7 mJ cm-2

 

CONCLUSION

FlexPDE® was used to numerically solve the TTM describing the ultrafast dynamics of optically excited electrons in thin metal films under laser heating. Using FlexPDE® to solve the TTM greatly reduced software development overheads and improved flexibility. Offering noncomputer specialists an easy means to model their experiment, FlexPDE® has much to offer to the experimenter in the investigation of energy transfer in single or multilayer metals during short pulse laser heating. FlexPDE version 4.0 is available in three license configurations. The evaluation and the student configuration are free. A vast number of meaningful problems of science and engineering can be addressed within the limits of these configurations19. The professional configuration offers the full power of FlexPDE version 4. It has effectively unlimited mesh size and unlimited number of simultaneous equations19. Reducing software development time and improving flexibility, FlexPDE® proved to be a valuable tool in modeling heat transfer mechanisms in thin metal films under ultrafast laser irradiation.

 

ACKNOWLDGMENT

The author wishes to acknowledge Dr. Carl E. Bonner, Jr. for the use of the femtosecond laser at Norfolk state University to perform the experimental part of this paper.

 

 

REFERENCES

[1]          G. L. Eesley, “Observation of Nonequilibrium Electron Heating in Copper,” Physical Review Letters, Vol. 51, 1983, pp. 2140-2143.

[2]          G. L. Eesley,  “Generation of nonequilibrium electron and lattice temperatures in copper by picosecond laser pulses,” Physical Review B, Vol. 33, 1986, pp. 2144-2151.

[3]          H. E. Elsayed-Ali, T. B. Norris, M. A. Pessot, and G. A. Mourou, “Time-resolved observation of electron-phonon relaxation in copper,” Physical Review Letters, Vol. 58, 1987, pp. 1212-1215.

[4]        H. E. Elsayed-Ali, and T. Juhasz, “Femtosecond time-resolved thermomodulation of thin gold films with different crystal structures,” Physical Review B, Vol. 47, 1993, pp. 13599-13610.

[5]          H. Inouye, K. Tanaka, I. Yanahashi, K. Hirao, “Ultrafast dynamics of nonequilibrium    electrons in a gold nanoparticle system,” Physical Review B, Vol. 57, 1998, pp. 11334-   11340.

[6]                  R. H. M. Groeneveld, R. Sprik and Ad Lagendijk, “ Femtosecond spectroscopy of      electron-electron and electron-phonon energy relaxation in Ag and Au,” Physical Review      B, Vol. 51, No. 17, 1995, pp 11433-11445.

[7]          J. Cao, Y. Gao, H. E. Elsayed-Ali, D. A, Mantell, “Femtosecond photoemission study of ultrafast electron dynamics on Cu(100),” Physical Review B, Vol. 56, 1997, pp.1099-1102.

[8]          S. Ogawa, H. Nagano, and H. Petek, “Optical Dephasing in Cu(111) Measured by Interferometric Two-Photon Time-Resolved Photoemission,” Physical Review Letters, Vol. 78, 1997, pp.1339-1342.

[9]               S. Ogawa, H. Nagano, H. Petek, “Hot-electron dynamics at Cu(100), Cu(110), and     Cu(111) surfaces: Comparison of experiment with Fermi-liquid theory,” Physical Review             B, Vol. 55, 1997, pp.10869-10877.

[10]       S.D. Brorson, A. Kazeroonian, J. S. Moodera, D. W. Face, T. K. Cheng, E. P. Ippen,

            M. S. Dresselhaus, and G. Dresselhaus, “Femtosecond room-temperature measurement of the electron-phonon coupling constant gamma in metallic superconductors,” Physical Review Letters, Vol. 64, 1990, pp. 2172-2175.

[11]       R. Rosei, and D. W. Lynch, “Thermomodulation Spectra of Al, Au, and Cu,” Physical             Review B, Vol. 5, 1972, pp. 3883-3894.

[12]              S.I. Anisimov, B. L. Kapelovich, and T. LO. Perelman, “Electron emission from metal   surfaces exposed to ultrashort laser pulses,” Soviet Physics – JETP, Vol. 39, 1974, pp.      375-377.

[13]       T. Q. Qiu, C. L. Tien, “ Short-pulse laser  heating on metals,” International Journal of            Heat and mass Transfer, Vol. 35, 1992, pp. 719-726.

[14]       T. Q. Qiu, C. L. Tien, “Heat transfer mechanisms during Short-pulse laser heating of      metals ,”Journal of Heat Transfer, Vol. 115, 1993, pp. 835-841.

[15]       T. Q. Qiu, C. L. Tien“ Femtosecond laser heating of multi-layer metals_ II. Experiments,”             International Journal of Heat and mass Transfer,Vol. 37, 1994, pp. 2789-2797.

[16]       C. K. Sun, F. Vallee,, L. Acioli, E. P. Ippen, and J. Fujimoto, “Femtosecond tunable measurement of electron thermalization in gold,”  Physical Review B 50, 1994, p. 15337.

[17]       W. S. Fann, R. Storz, H. W. K. Tom, and J. Bokor, “Direct measurement of    nonequilibrium electron-energy distributions in subpicosecond laser-heated gold films,” Physical Review Letters, Vol. 68, 1992, pp. 2834-2837.

[18]       W. S. Fann, R. Storz, H. W. K. Tom, and J. Bokor, “Electron Thermalization in Gold,” Physical Review B 46, 1992, pp. 13592-13595.

[19]       FlexPDE®, http://www.pdesolutions.com, User Manual, PDE Solutions Inc., P.O.Box   4217, Antioch, CA 94531.

[20]      Gray, D.E., ed., American Institute of Physics Handbook, 3rd ed., New York: McGraw-       Hill, 1972.

[21]         Wael M. G. Ibrahim, H. ElSayed-Ali, C. E. Bonner, and M. Shinn, “Ultrafast    investigation of electron dynamics in multi-layer metals,” International Journal of Heat       and Mass Transfer, Vol. 47, No. 10-11, 2004, pp. 2261-2268.

[22]      Wael M. G. Ibrahim: Ph.D Thesis, “Study of Non-equilibrium Electron dynamics in        Metals,” Old Dominion University, 2002.